第十六章 数学实验室(二):绘制函数曲线
在上一章中,通过编写程序解决了几个算术问题,并借此展示了将实际问题转化为数学问题,再将数学问题转化为程序问题的思路。本章将继续讨论有关数学问题——通过编程绘制函数曲线,内容涉及到中学数学中的函数及平面直角坐标系等相关知识,对于尚未学习这项内容的读者来说,建议首先了解相关知识。
第一节 坐标变换
一、画布坐标系统
在App Inventor中创建一个新项目——画布坐标,在设计视图中,设置Screen1的标题属性为“画布坐标”,水平对齐属性为居中;拖入一个画布组件,设置其宽、高均为300像素,画笔线宽为1,并添加标签、文本输入框及按钮组件,如图16- 1所示。
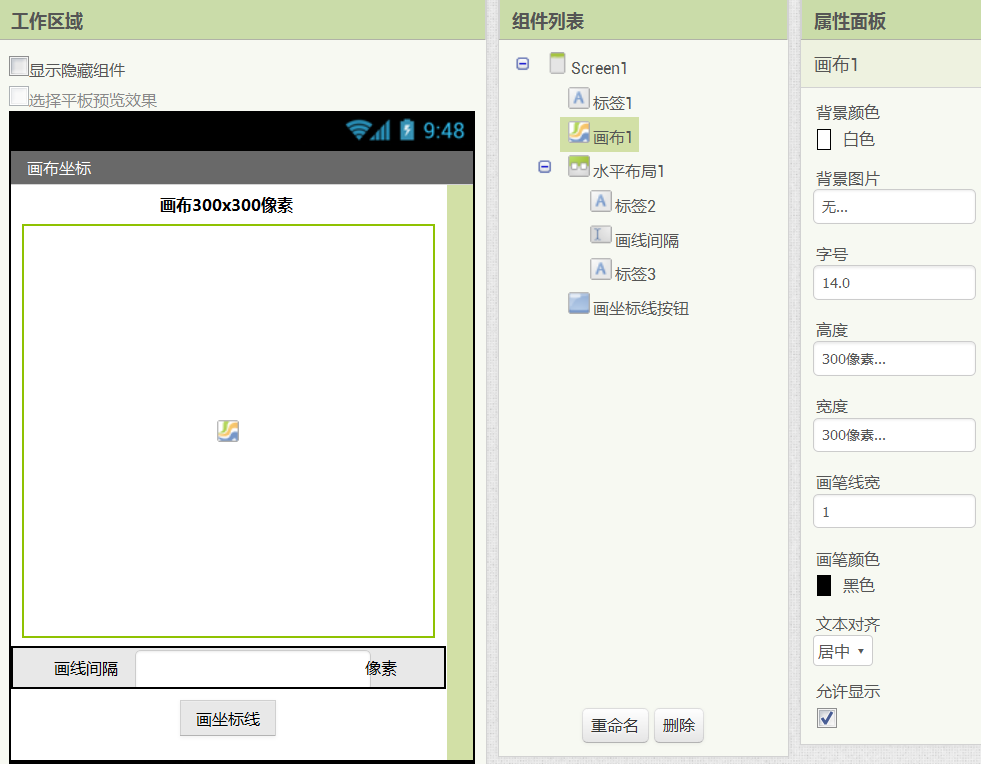 图16-1 创建一个名为“画布坐标”的项目,并添加画布、输入框、按钮及标签等组件
图16-1 创建一个名为“画布坐标”的项目,并添加画布、输入框、按钮及标签等组件为了对画布的长度单位——像素有一个感性的认识,我们在画布上分别沿水平及垂直方向,每隔一定距离画一条线,线与线之间的距离由用户在文本输入框“画线间隔”中输入。绘制直线的代码如图16- 2所示。
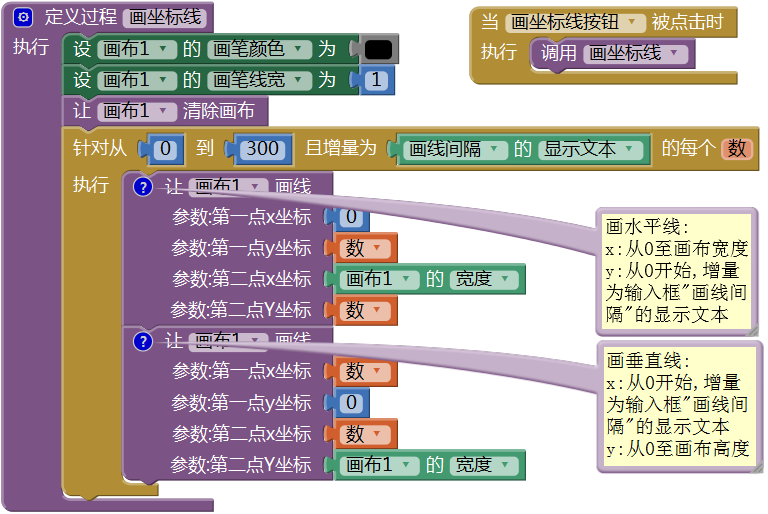 图16-2 在画布上每隔一定距离绘制水平线及垂直线
图16-2 在画布上每隔一定距离绘制水平线及垂直线程序的执行结果如图16- 3所示。用户在“画线间隔”输入框中输入不同的数值,然后点击画坐标线按钮。注意观察平行线之间距离随“画线间隔”的变化。图中特别保留了手机的状态栏,这些现实世界中的真实参照物,可以帮助读者建立起关于像素尺寸的空间感。另外,画布上方的标签显示了画布的宽度和高度,其中文字的字号为14,不妨对比一下,看哪一张图中的方格大小更接近14号字的大小,以便在头脑中形成对像素大小的认识。在左上角的图中,我们用红色文字标注了几个关键点的坐标,值得注意的是,画布坐标系统的原点在画布的左上角,也就是说,y轴的正方向指向下方,这是与数学中的平面直角坐标最大的不同。
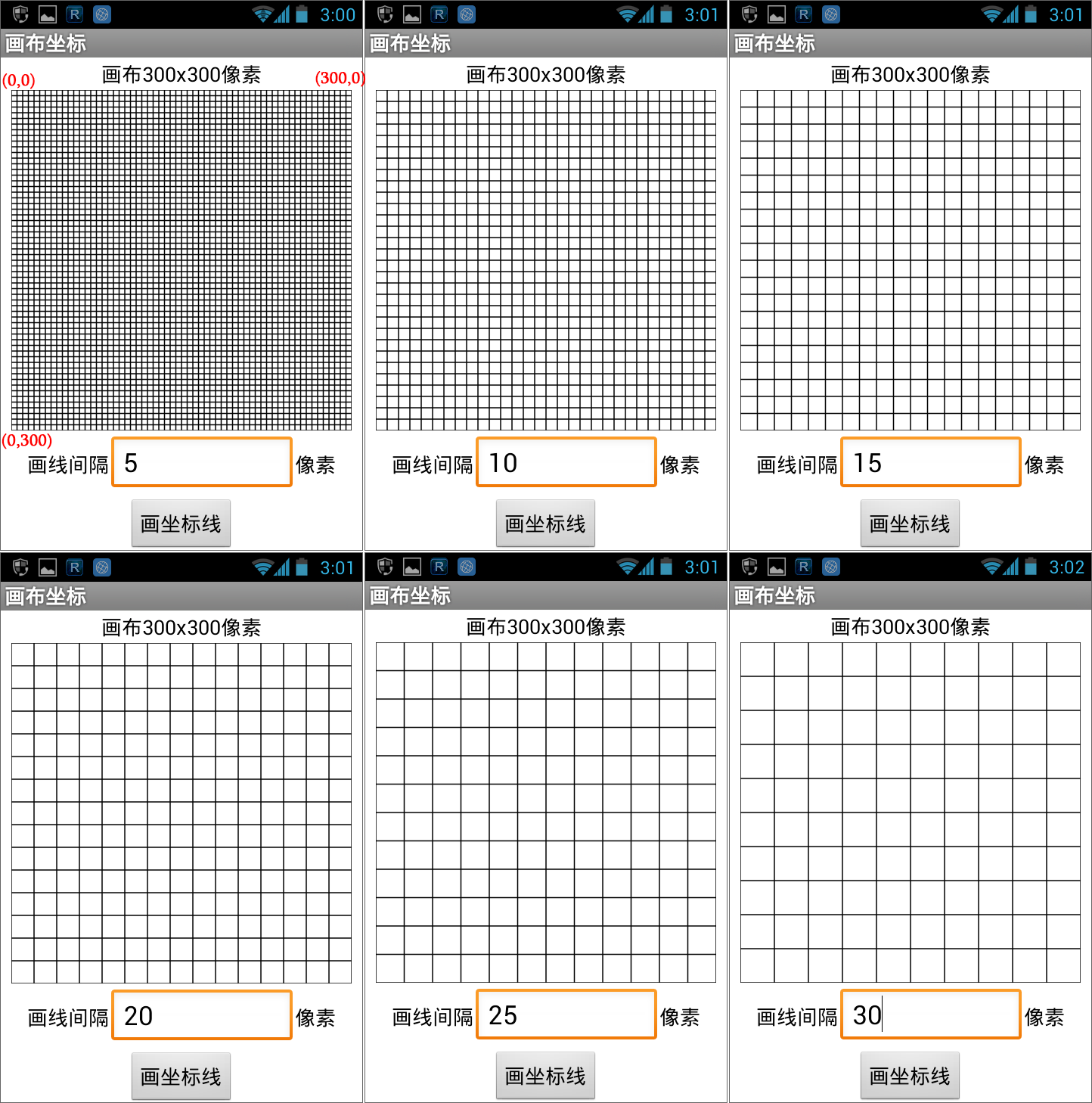 图16-3 画布坐标系统
图16-3 画布坐标系统二、平面直角坐标系
绘制上述图形的另一个目的,是为了最终绘制我们需要的平面直角坐标。在数学中,一个坐标系统中包含坐标轴(带有正方向箭头的直线)、单位标记以及标注数字,而且y轴的正方向指向上方。我们以图16- 3中右下角的图(画线间隔为30像素)为背景,在Photoshop中绘制了四个典型的平面直角坐标,如图16- 4所示。图中的黑色文字用于描述画布坐标系统,红色文字用于描述平面直角坐标系统。
 图16-4 原点位置不同的四个平面直角坐标
图16-4 原点位置不同的四个平面直角坐标我们以左上角的图(a)为例,解释图中标注的文字。首先确定两个最重要的名词:
- 画布坐标系统:图中黑色线条及文字描述的坐标系统,原点位于画布左上角,水平方向为x轴,正方向指向右方,垂直方向为y轴,正方向指向下方,单位为像素,x及y轴最大标注值为300,标注间隔为30像素;
- 平面直角坐标系统:图中红色线条及文字描述的坐标系统,原点位于画布的左下角,距画布的左边界及下边界均为30像素,x轴正方向指向右方,y轴正方向指向上方,1个单位为15像素,x轴及y轴的最大标注值均为18,标注间隔为2(2个单位=30像素)。
下面解释图中标注文字的含义:
- (X0,Y0):平面直角坐标的原点在画布坐标系统中的坐标,图(a)中原点坐标为(30,270)。
- P:图中的红点,平面上的任意一点;
- (cx,cy):P点在平面直角坐标系中的x、y坐标,也称作计算坐标,图(a)中P点的计算坐标为(8,12);
- (dx,dy):P点在画布坐标系中的x、y坐标,也称作绘图坐标,图(a)中P点的绘图坐标为(150,90);
- 比例:平面直角坐标系中的1个单位与画布坐标系中1个单位之间绝对长度的比值,即,1个平面直角坐标单位所包含的像素数,x轴与y轴的比例可以相同,也可以不同,四幅图中x轴及y轴的比例均为15;
- 标注间隔:平面直角坐标系中,两个标注数字之间的间隔,以平面直角坐标系中的单位为计量单位,四幅图中x轴及y轴的标注间隔均为2。
图16- 4中绘制了四个平面直接坐标,它们的区别在于对称性,这里所说的对称性,是指在画布的可视范围内,坐标轴的对称性。下面分别加以解释:
- 非对称坐标:如图(a)所示,只保留了平面直角坐标系的第一象限,用于绘制x、y值均大于等于0的图形,例如 y=√x 。
- 关于y轴对称:如图(b)所示,保留了平面直角坐标系中的第一、二象限,用于绘制y≥0的图形,例如y=x2 ;
- 关于x轴对称:如图(c)所示,保留了平面直角坐标系中的第一、四象限,用于绘制x≥0的图形,例如 y=sinx,当x取值范围在[0,2π]时;
- 关于原点对称:如图(d)所示,完整地保留了平面直角坐标系的四个象限,可以绘制任意类型的函数曲线。
三、两个坐标系之间的坐标变换
在图16- 4的四个平面直角坐标中,有一个相同的部分,就是坐标转换公式:
dx = X0 + cx
dy = Y0 – cy
我们已经在上一个标题中解释了公式中各项的含义,现在来说明这些数据的来源。计算坐标(cx,cy)来自于对曲线方程的计算,以 y=x2为例,cx的值由绘图程序自动生成(循环语句中的循环变量),它们可以是0、1、2等间隔相等的整数,也可以是0、0.5、1、1.5这样间隔相等的小数;cy的值通过对函数的计算求得,对于二次函数y=x2,对应于0、1、2这样的cx值,cy的值为0、1、4等;又比如,对于三角函数y=sinx,cx的值可以设为0、1、2(单位为角度)等,cy的值可以用App Inventor中的正弦函数求得(sin1°、sin2°、sin3°等)。
有了计算坐标,就可以利用坐标变换公式求出绘图坐标,因此也就可以实现在画布上绘图的目标。关于坐标变换公式,读者如果有兴趣,可以在不同的坐标系中,在平面上随便找一个点,来验证公式的正确性。
第二节 绘制坐标轴
在上一节中,图16- 4中的四个平面直角坐标并不是在App Inventor中用程序绘制出来的,而是在Photoshop中画出来的。在正式开始绘制函数曲线之前,我们要亲手绘制坐标轴、确定坐标轴长度单位的比例以及标记数字的间隔,而这些因素与我们要绘制的曲线有关。
以二次曲线y=x2为例,假设x的取值范围为[-10.10](共20个单位),则y的取值范围为[0,100](100个单位)。为了充分利用画布有限的绘图空间(300x300像素),选择图16- 4(b)作为绘图坐标,并设x轴的比例为15(1个单位=15像素,300像素被均分为20个单位),y轴的比例为2.5(1个单位=2.5像素,300像素被均分为120个单位);同时,对于坐标轴上标注的数字,也要加以考虑:对于x轴,比较适宜的标注间隔是2个单位(30像素),对于y轴,适宜的标注间隔为10个单位(25像素)。
上面的分析为绘制坐标轴提供了足够的依据,其中包含下列要素:
- 原点坐标(X0,Y0);
- 坐标轴的单位比例:比例X、比例Y;
- 坐标轴标注间隔:标注间隔X、标注间隔Y。
有了这些要素,我们就可以绘制出满足绘图要求的坐标轴,继而就可以绘制对应的曲线。下面我们回到App Inventor中,用程序来绘制坐标轴。
一、界面设计
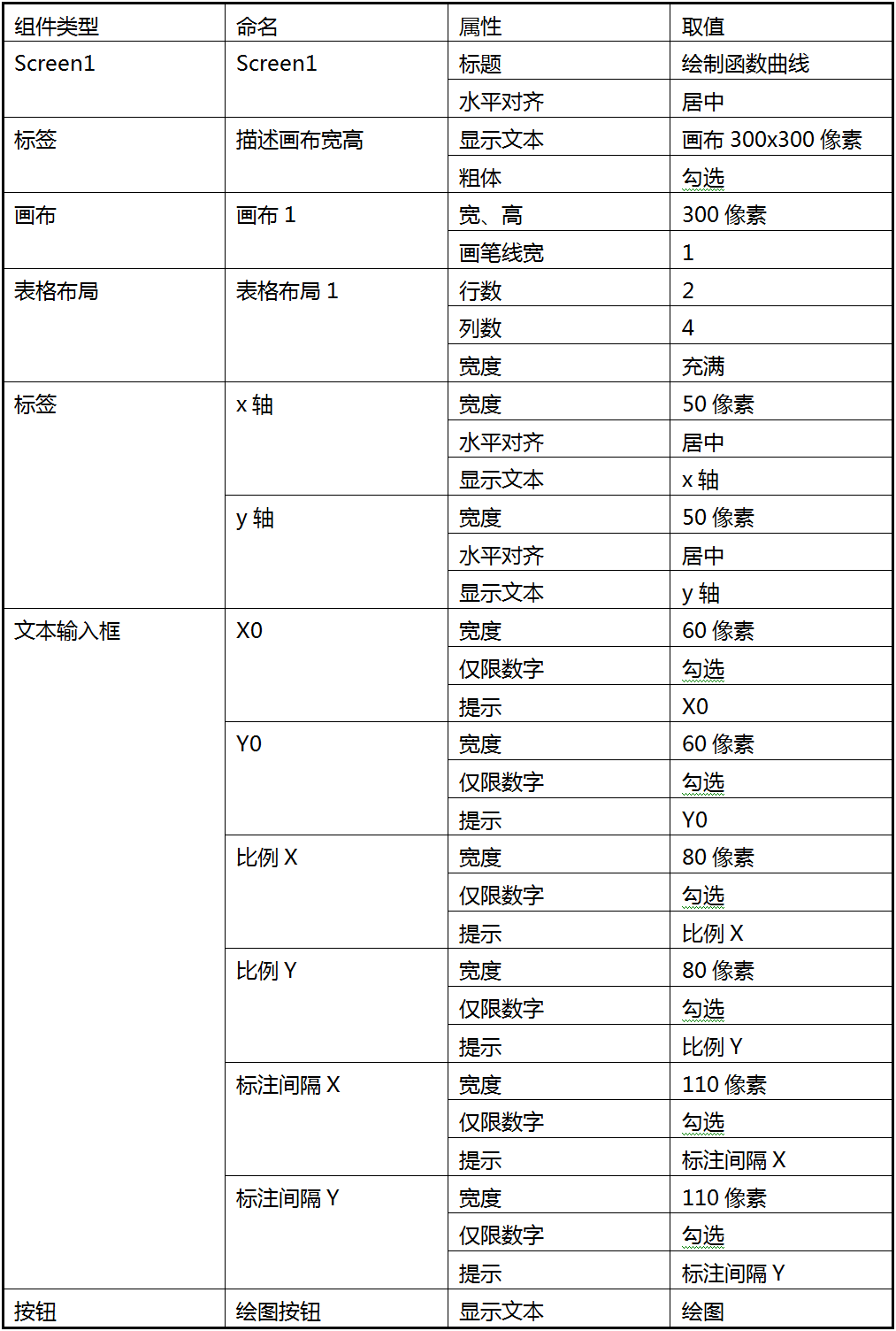
在App Inventor中创建新项目“绘制函数曲线”,用户界面如图16- 5所示,其中的组件设置如表16- 1所示。
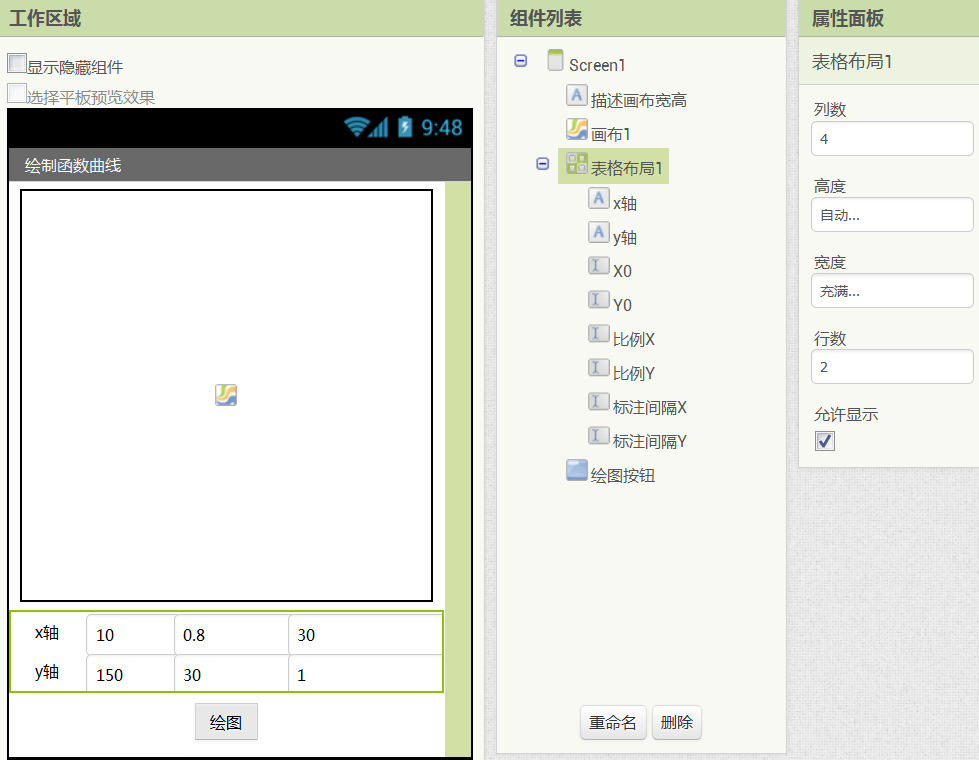 图16-5 新建项目“绘制函数曲线”的用户界面
图16-5 新建项目“绘制函数曲线”的用户界面表16- 1 项目“二次函数曲线”中组件的设置
二、编写代码
1、绘制坐标轴
在用户界面中有6个文本输入框,用来设定平面直角坐标系的原点坐标、坐标轴单位的比例以及数字的标注间隔,我们先来绘制坐标轴。代码如图16- 6所示。
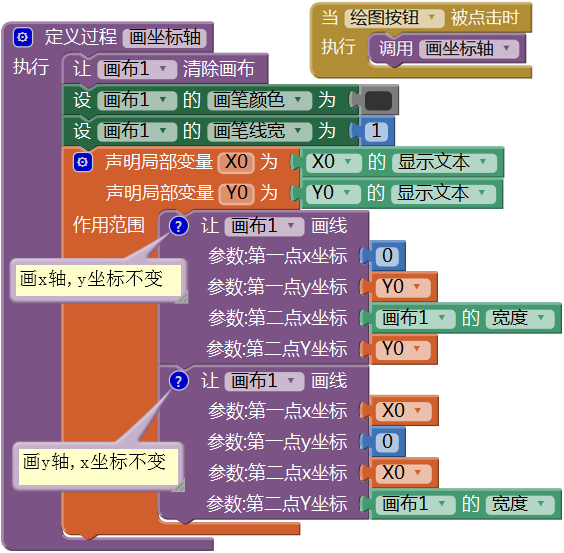 图16-6 绘制坐标轴
图16-6 绘制坐标轴在用户界面上输入不同的X0、Y0值,将得到不同的坐标轴,测试结果如图16- 7所示。
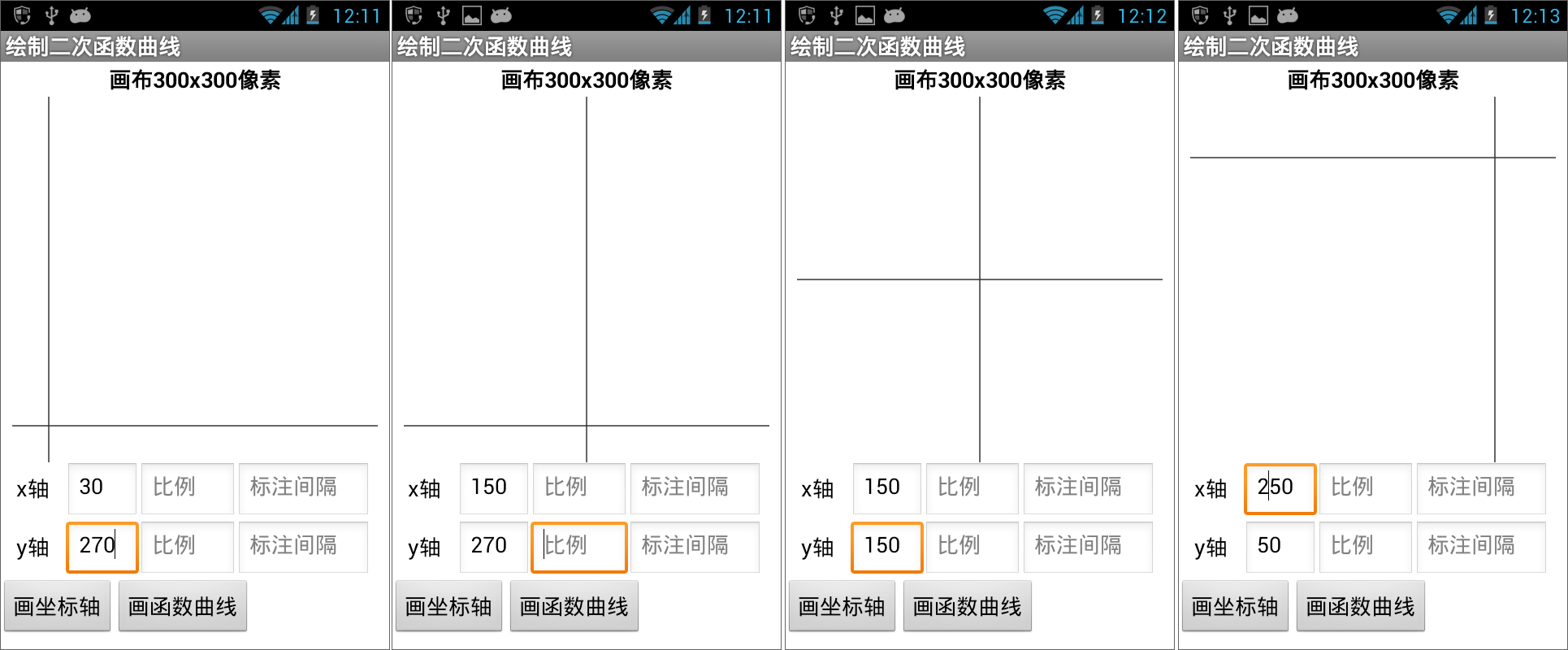 图16-7 测试——在画布的不同位置用程序绘制坐标轴
图16-7 测试——在画布的不同位置用程序绘制坐标轴2、坐标轴的标注
首先对x轴进行标注,以原点为0点,向左标注负数,向右标注正数,代码如图16- 8所示。
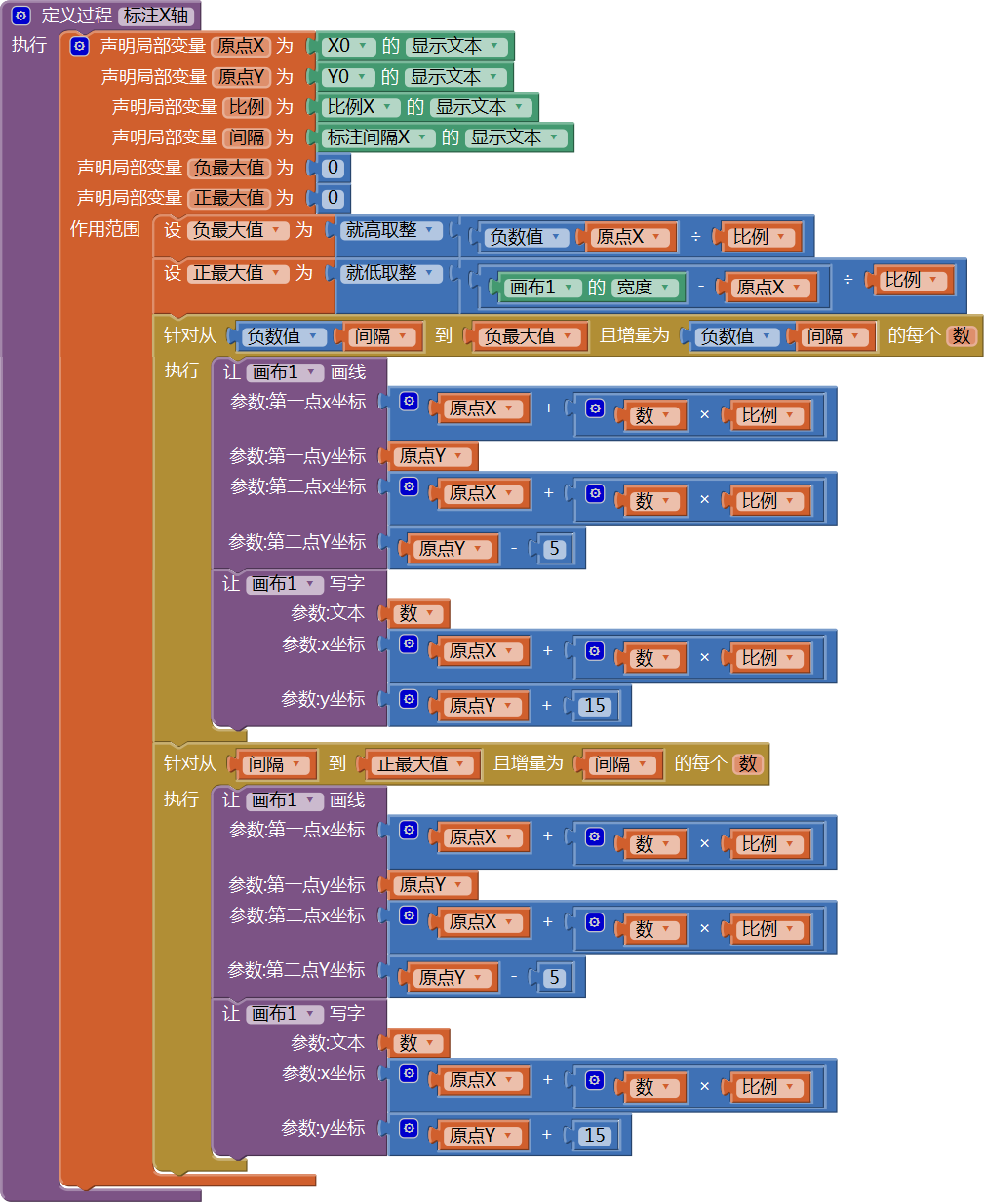 图16-8 过程——标注X轴
图16-8 过程——标注X轴注意图中两个循环语句的起始值,标注负数时,以“负间隔”为起点,标注正数时,以“间隔”为起点,这里省略了对零点的标注,稍候你将看到这样标注的原因。
上图中两个循环语句内部的代码完全相同,为了提高代码的复用性及可维护性,我们将这部分相同的代码封装成过程,改造后的代码如图16- 9所示。
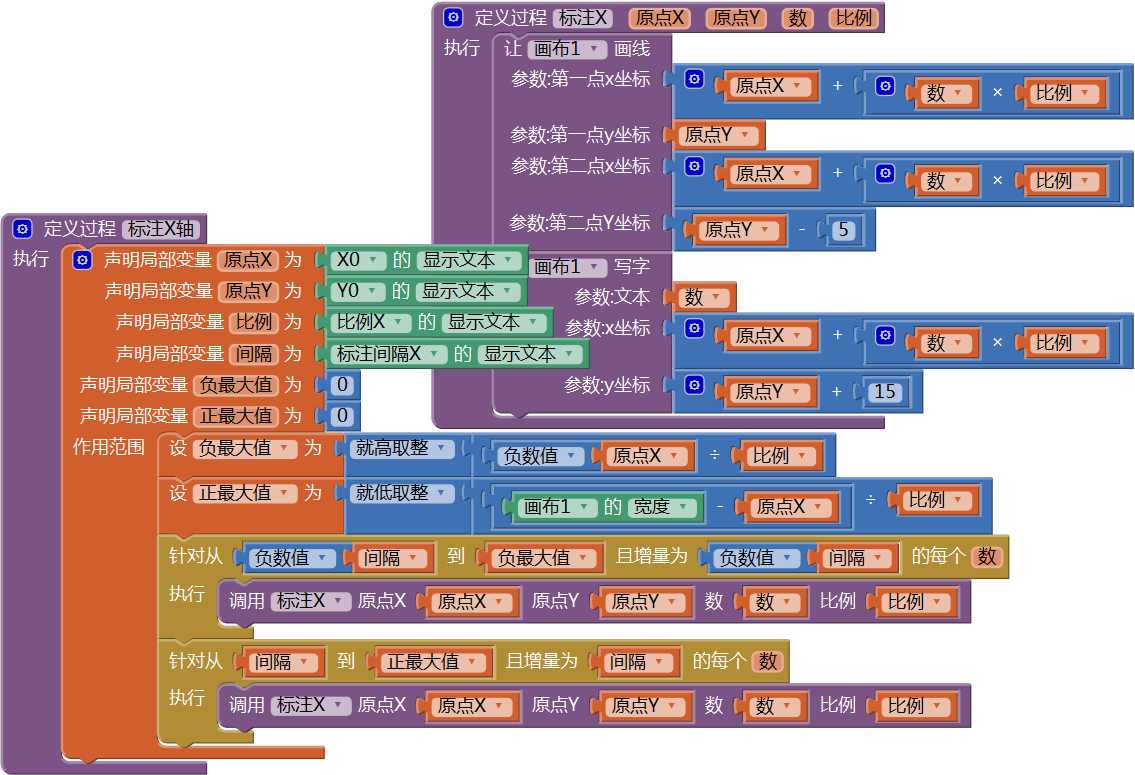 图16-9 创建“标注X”过程,并改造“标注X轴”过程
图16-9 创建“标注X”过程,并改造“标注X轴”过程接下来用同样的思路对y轴进行标注,代码如图16- 10所示。
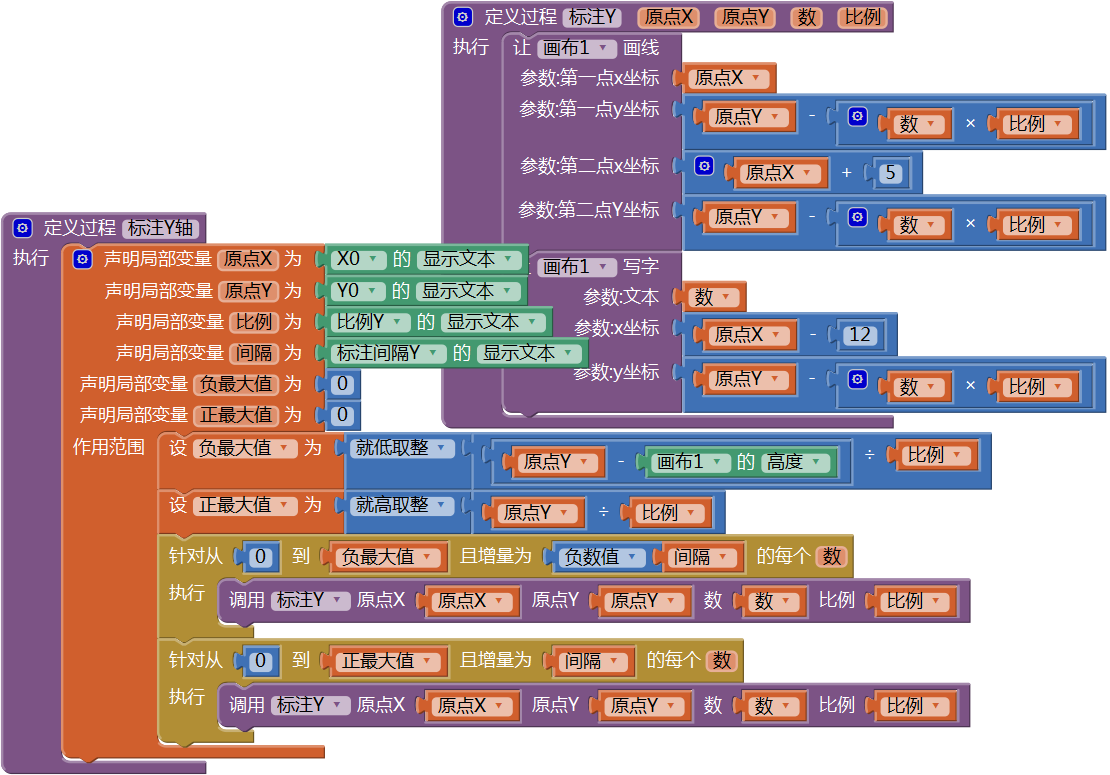 图16-10 在“标注Y轴”过程中调用“标注Y”过程
图16-10 在“标注Y轴”过程中调用“标注Y”过程注意到图中两个循环语句的循环变量初始值均为零(其实只要有一个为零即可),这个零既是x轴的零点,也是y轴的零点,这就是“标注X轴”过程里循环语句起始值不为零的原因。下面在绘图按钮的点击程序中调用上述过程,如图16- 11所示,测试结果如图16- 12所示。
 图16-11 调用两个“标注”过程
图16-11 调用两个“标注”过程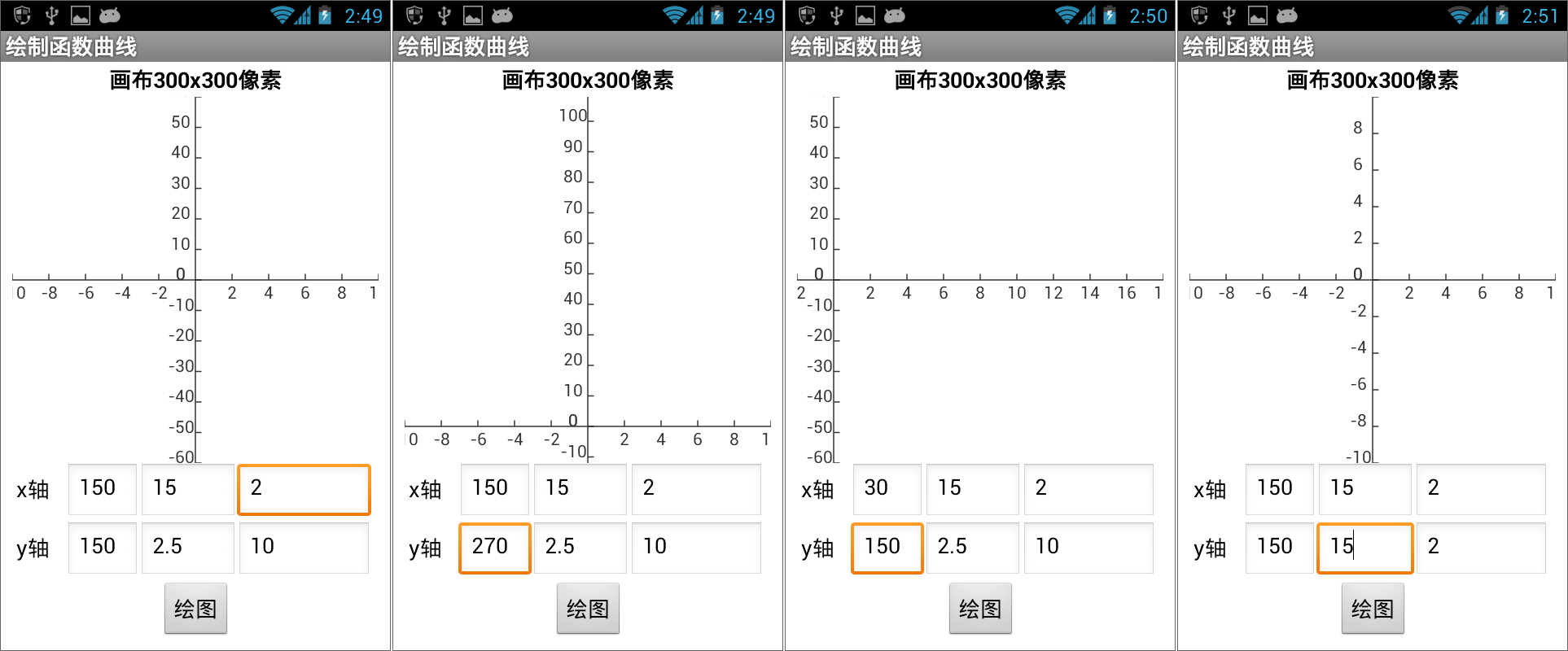 图16-12 测试——绘制坐标轴并标注数字
图16-12 测试——绘制坐标轴并标注数字通过设置不同的原点坐标、单位比例及标注间隔,我们获得了不同的坐标轴,下面我们将选择合适的坐标轴来绘制不同类型的函数曲线——二次曲线及三角函数曲线。
第三节 绘制二次函数曲线
一、绘制最简单的二次曲线
标准的二次函数可以写为y=ax2+bx+c,我们将从最简单的y=x2开始,然后通过设置不同的a、b、c值来观察曲线随系数的变化。
App Inventor并不具备绘制曲线的功能,所谓曲线,实际上是由一系列的微小线段拼接而成。我们选择图16- 12中的左二图为绘图坐标,来绘制y=x2曲线。
在图16- 4中我们引入了计算坐标及绘图坐标的概念,并给出了它们之间的换算关系:
dx = X0 + cx
dy = Y0 – cy
关于计算坐标的来源,首先需要确定cx的取值范围(数学中所说的函数的定义域),然后设定cx的增量,这两个因素确定后,利用循环语句,就可以获得cx的具体值,然后根据y=x2来求cy值,这样就有了计算坐标(cx,cy),再根据上述换算公式,求得对应的绘图坐标,并利用两个这样的绘图坐标来绘制微小线段,组成一条完整的曲线。
首先创建两个有返回值的过程——绘图坐标X及绘图坐标Y,将计算坐标换算为绘图坐标,代码如图16- 13所示。
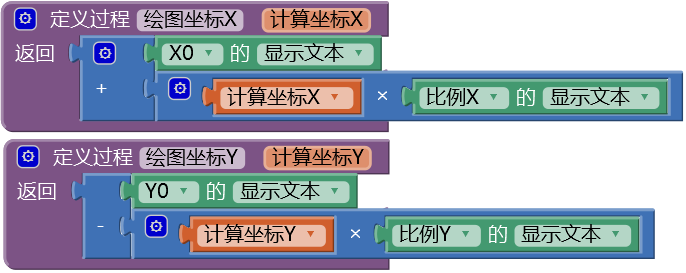 图16-13 将计算坐标换算为绘图坐标的过程
图16-13 将计算坐标换算为绘图坐标的过程然后,创建一个过程——绘制二次函数曲线,并在绘图按钮点击程序中调用该过程,来实现曲线的绘制,代码如图16- 14所示,测试结果如图16- 15所示。
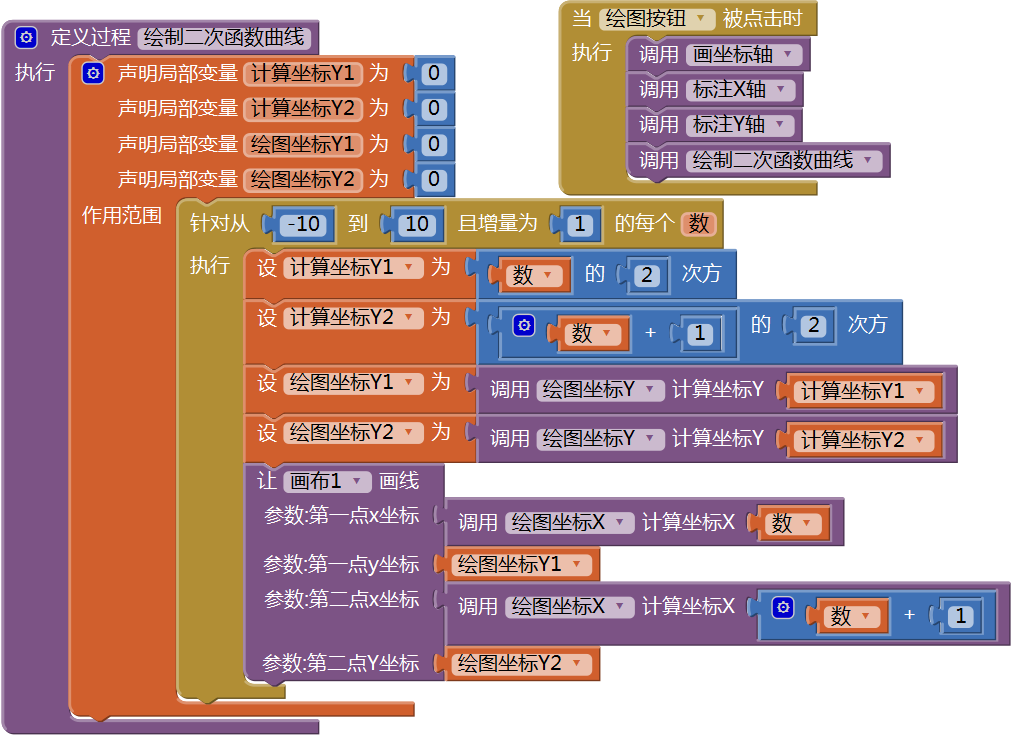 图16-14 在按钮点击程序中调用“绘制二次函数曲线”过程
图16-14 在按钮点击程序中调用“绘制二次函数曲线”过程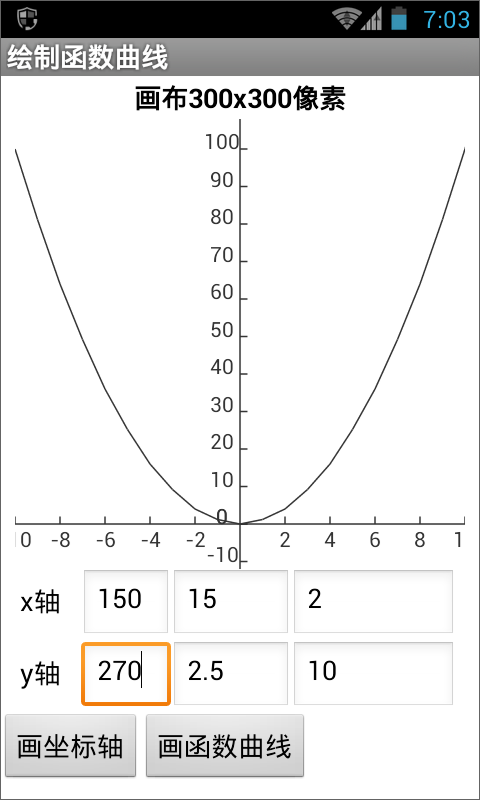 图16-15 绘制二次函数曲线的测试结果
图16-15 绘制二次函数曲线的测试结果如果仔细观察,会发现这条曲线不够平滑,尤其在x=±2时,能看到折线的痕迹。可以通过缩小x的增量,即,循环语句中的增量值,来增加曲线的平滑度,如,设增量为0.5或更小。
二、绘制任意系数的二次曲线
图16- 15中是一条最简单的二次曲线,曲线方程中的系数a为1,b、c均为0。下面我们回到App Inventor的设计视图,将表格布局组件的行数由2改为3,向新增的第三行中添加一个标签及三个文本输入框,标签的显示文本设为“系数”,文本输入框分别命名为“系数a”、“系数b”及“系数c”,宽度均设为60像素,并勾选“仅限数字”选框。通过在输入框中输入不同的a、b、c值,来改变曲线的位置及形状。修改后的用户界面如图16- 16所示。为了能够显示新增的输入框及按钮组件,这里隐藏了屏幕顶端的“描述画布宽高”标签。
 图16-16 添加三个文本输入框,用来输入二次方程的系数
图16-16 添加三个文本输入框,用来输入二次方程的系数绘制带有系数的二次曲线,最困难的是坐标轴的确定,也就是原点位置的确定。为了简化程序,我们将坐标原点设在画布的中心,即(150,150)点,以固定的坐标轴来绘制不同的曲线。
首先创建一个有返回值的过程——y,对给定的参数x,求ax2+bx+c的值,代码如图16- 17所示。
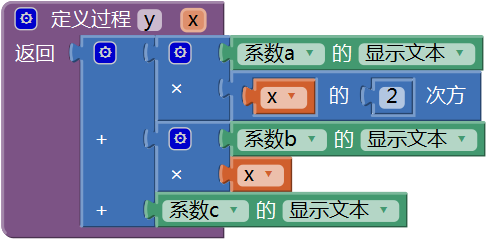 图16-17 有返回值的过程——y
图16-17 有返回值的过程——y然后改造“绘制二次函数曲线”过程,如图16- 18所示。
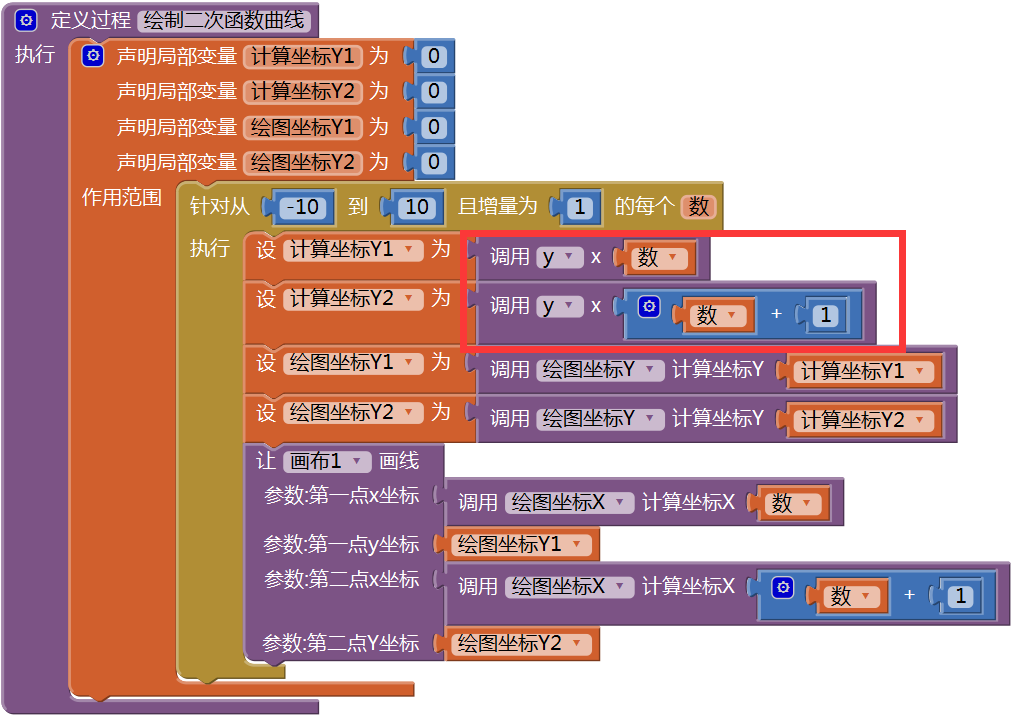 图16-18 可以绘制任何一个二次函数曲线的过程
图16-18 可以绘制任何一个二次函数曲线的过程为了测试上述程序,我们需要制定一个测试策略,即,每次只改变一个系数,另外两个系数保持不变,这样才能确定每个系数对曲线位置及形状的影响,测试结果如图16- 19、图16- 20及图16- 21所示。
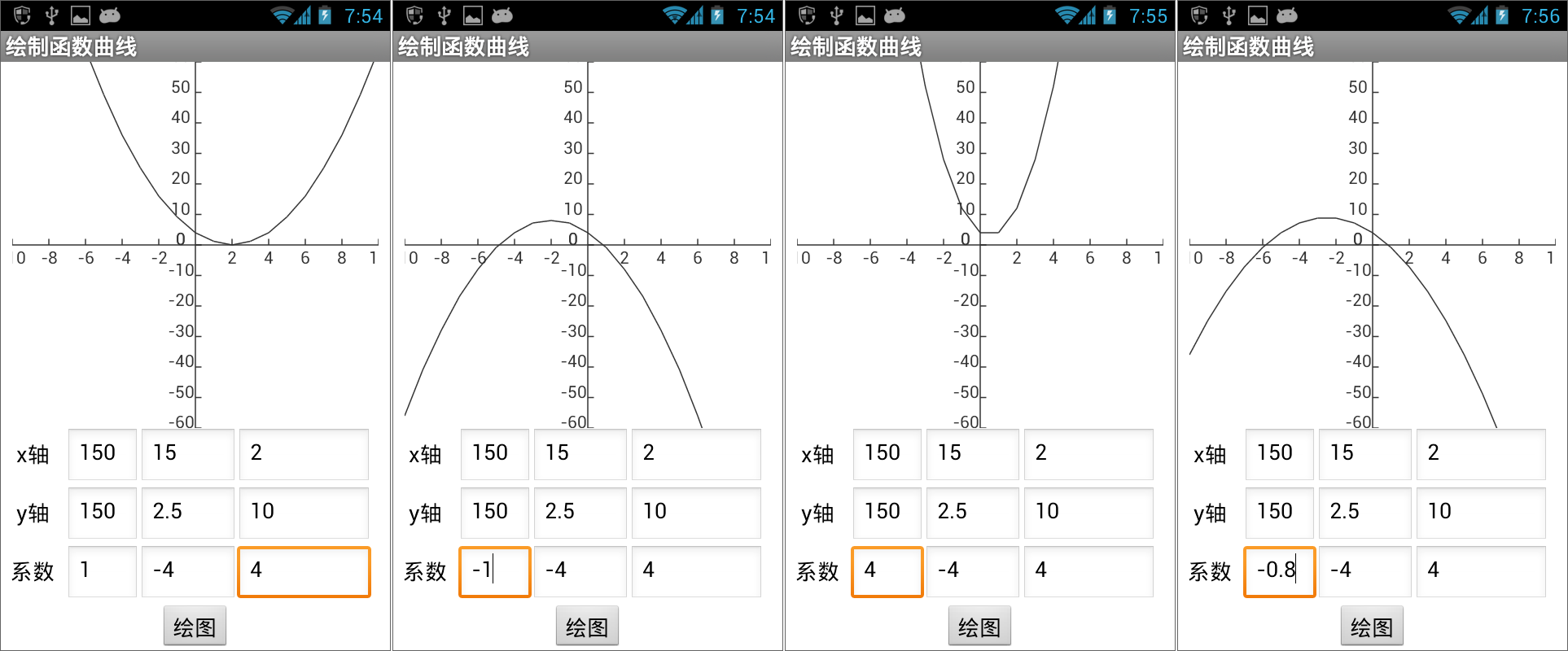 图16-19 带有系数的二次函数曲线——系数a对曲线的影响
图16-19 带有系数的二次函数曲线——系数a对曲线的影响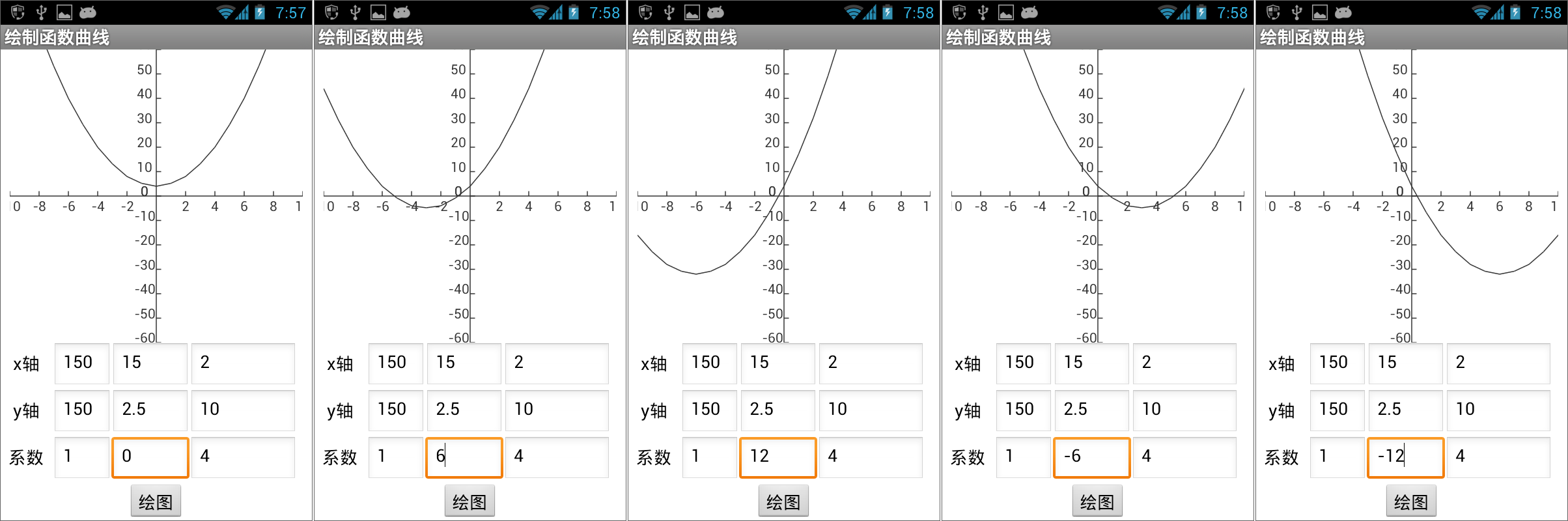 图16-20 带有系数的二次函数曲线——系数b对曲线的影响
图16-20 带有系数的二次函数曲线——系数b对曲线的影响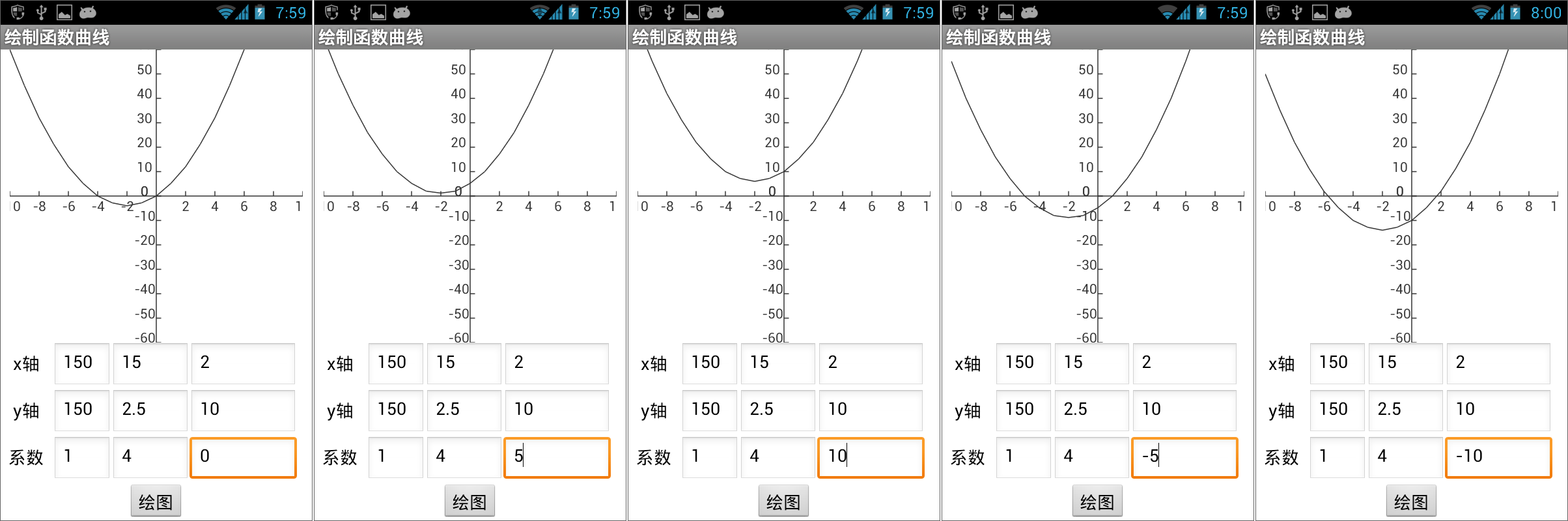 图16-21 带有系数的二次函数曲线——系数c对曲线的影响
图16-21 带有系数的二次函数曲线——系数c对曲线的影响三、连续改变系数值
1、使用数字滑动条
回到App Inventor设计视图,从用户界面组件中,将数字滑动条拖入到用户界面中,置于画布下方,设滑动条宽度为280像素,最小值为-20,最大值为20,滑块位置为0,如图16- 22所示。
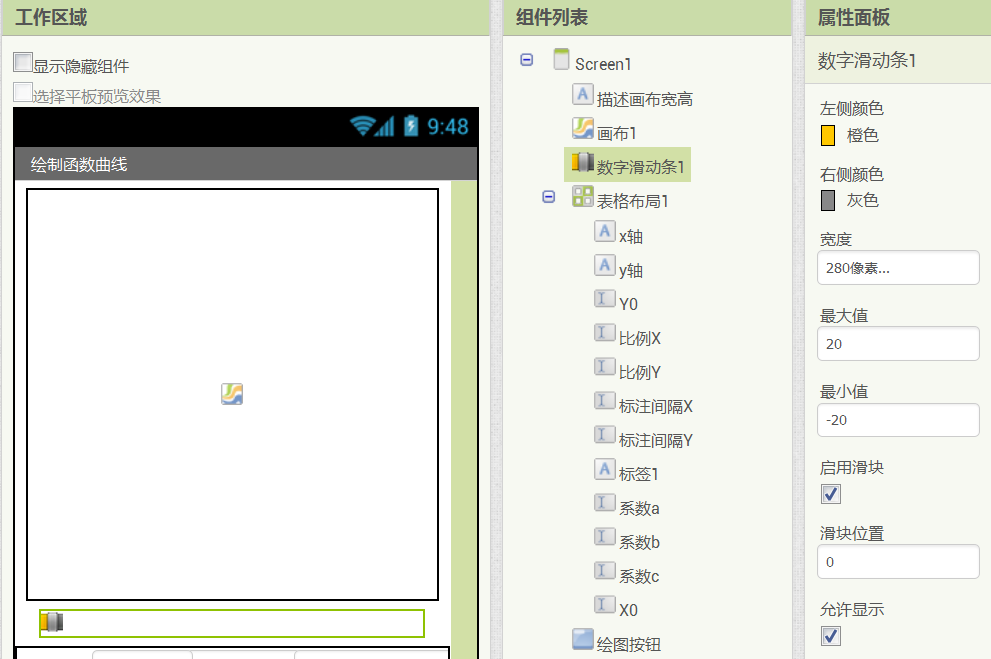 图16-22 添加数字滑动条组件
图16-22 添加数字滑动条组件在编程视图中改造过程y,并在滑动条的位置改变事件中,调用相关过程,代码如图16- 23所示。当滑块位置改变时,让文本输入框“系数a”显示滑块位置,将过程y中“系数a的显示文本”替换为“数字滑动条1的滑块位置”,这样,随着滑块位置的改变,应用将绘制不同的二次曲线。测试结果如图16- 24所示。
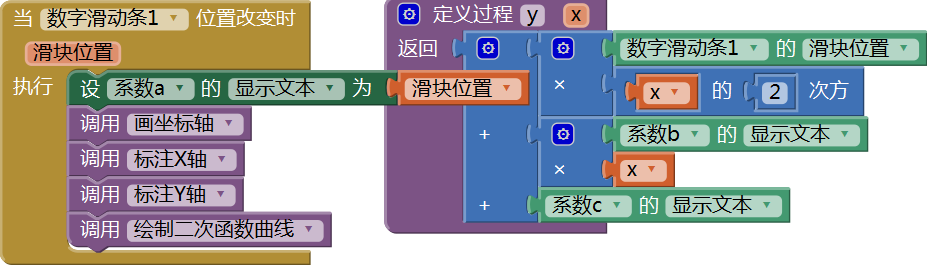 图16-23 利用滑块位置确定二次方程的系数a
图16-23 利用滑块位置确定二次方程的系数a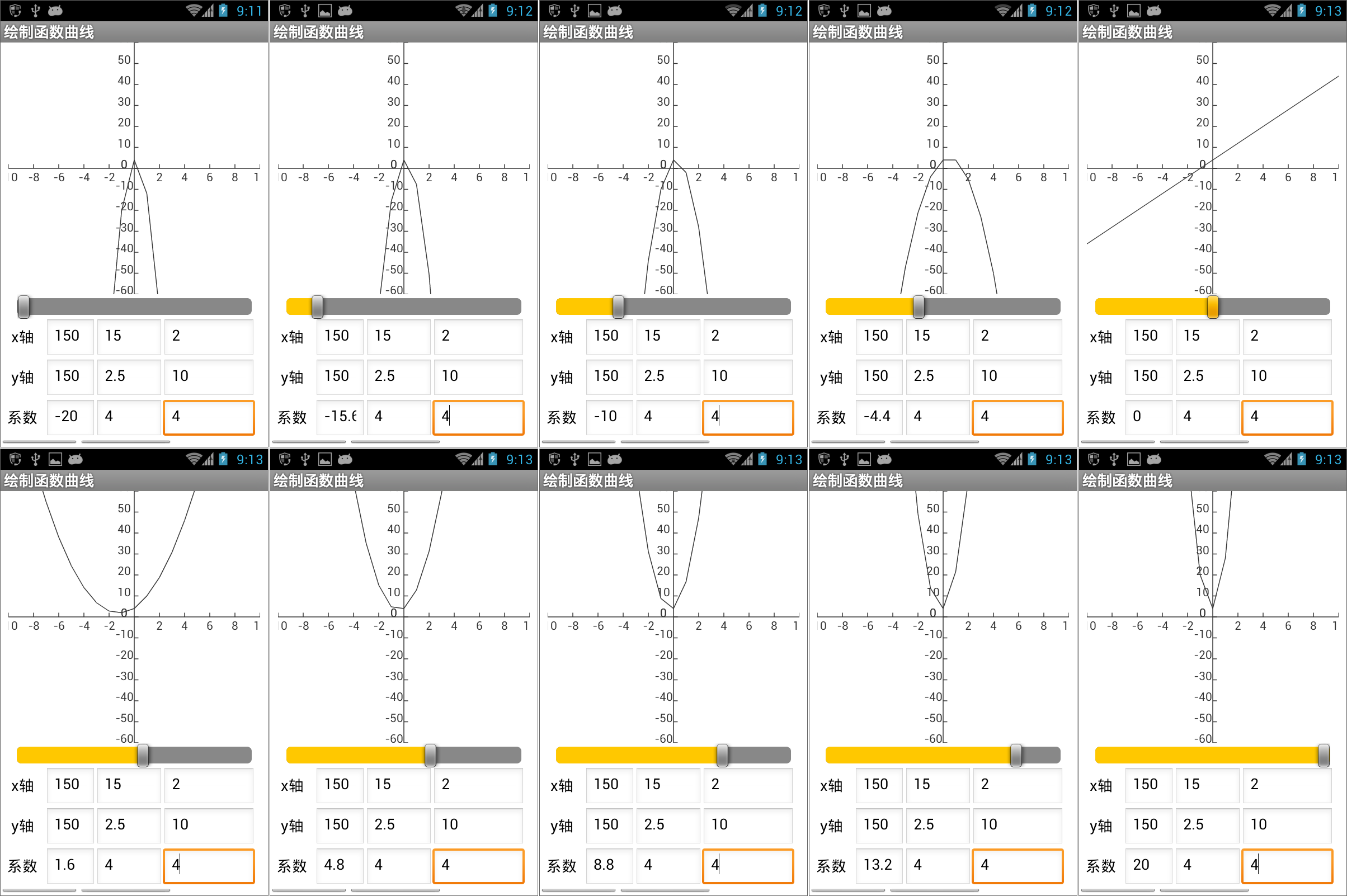 图16-24 用滑动条的滑块位置作为二次方程的系数a
图16-24 用滑动条的滑块位置作为二次方程的系数a在测试过程中,由于笔者的手机性能的原因,无法实现滑块位置的平滑改变,只能取几个点的值来获得对应的曲线,这个程序如果是在主流型号的计算机中运行,效果会更加理想,这里只是抛砖引玉,希望读者能够理解“数学实验室”的概念——利用程序实现函数曲线的绘制,通过连续改变函数的某个系数,来理解该系数对曲线形状及位置的影响。下面我们继续开拓思路,利用计时器组件的计时事件,来修改系数a的值,并触发绘图程序。
2、用计时器控制绘图速度
在设计视图中向项目中添加一个计时器组件,并设其计时间隔为2000毫秒(为了有足够的时间完成截图)。如图16- 25所示。
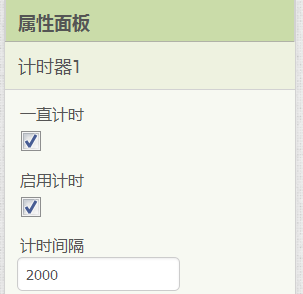 图16-25 为项目添加计时器组件,并设置其计时间隔为2000毫秒(2秒钟)
图16-25 为项目添加计时器组件,并设置其计时间隔为2000毫秒(2秒钟)在编程视图中,声明一个全局变量a,并设其初始值为-10,利用计时器的计时事件,来实现系数a的递增,并调用相关的绘图程序,实现曲线的绘制,具体代码如图16- 26所示。
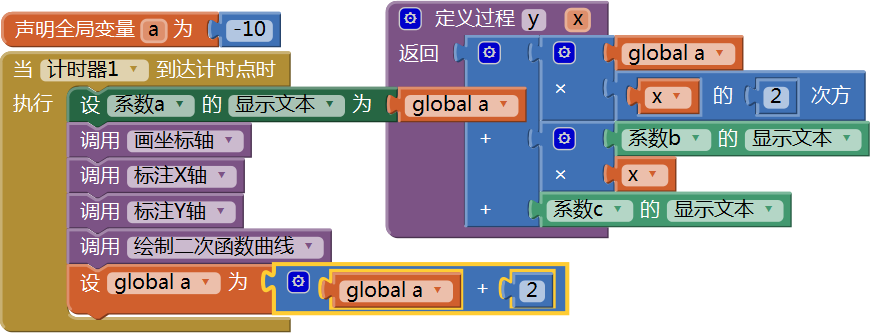 图16-26 利用计时器的计时事件来设置系数a的值,并调用相关的绘图过程
图16-26 利用计时器的计时事件来设置系数a的值,并调用相关的绘图过程由于计时器组件在程序开始运行时就已经启动计时,这样我们就来不及输入绘制坐标轴的参数以及二次方程的另外两个系数b、c,因此,我们在项目的设计视图中设置好这些文本输入框的显示文本属性,以便计时事件触发时,程序可以获取到必要的绘图数据。测试结果如图16- 27所示,没有来得及捕获第一张图(a=-10),第二张图中还残留了不小心碰到的音量调节指示条,从一系列连续取值的曲线图中,很容易发现系数a对曲线开口方向、顶点位置以及开口大小的影响,尤其是当a=0时,曲线方程变为直线方程,即y=4x+4。
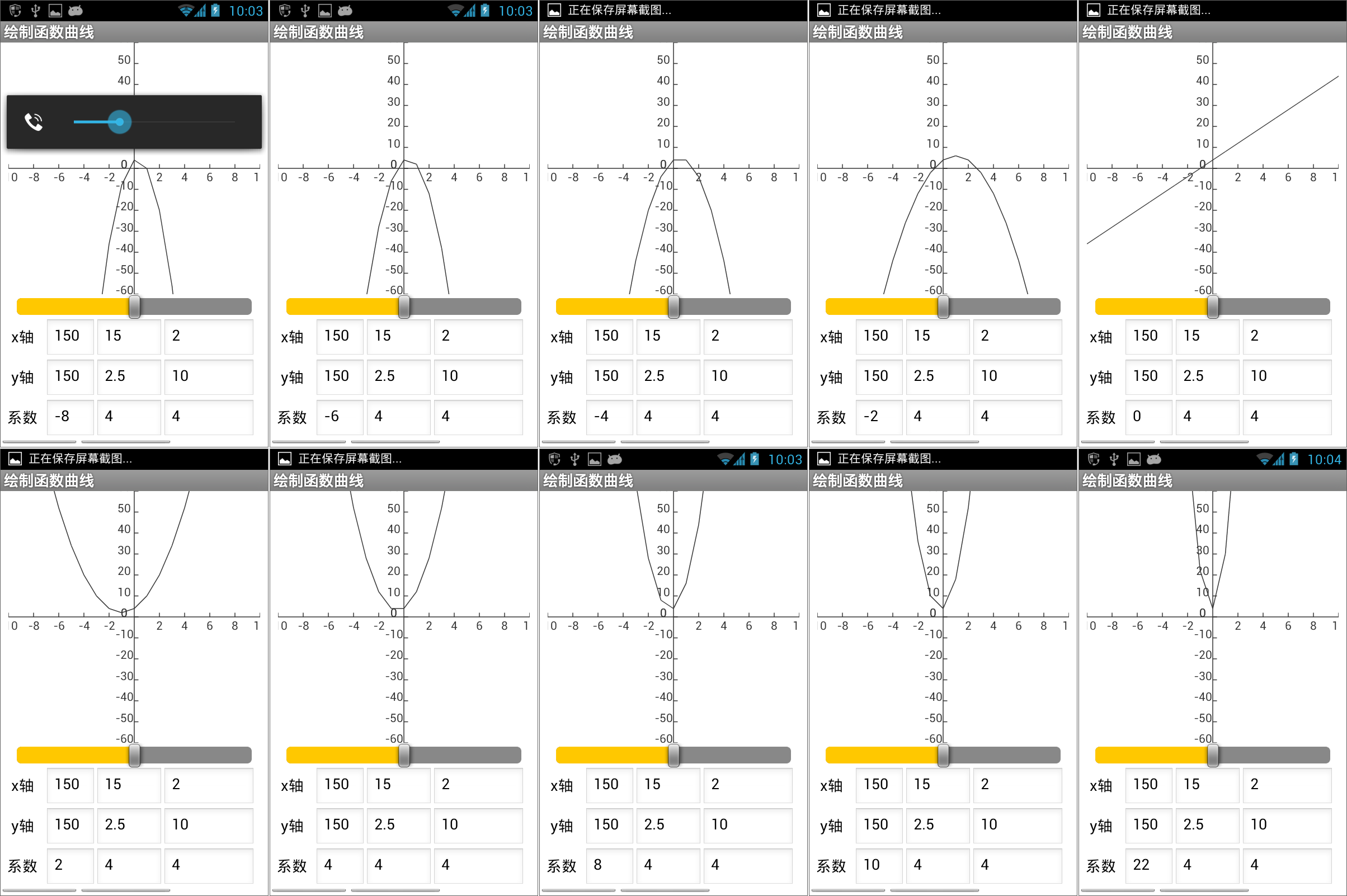 图16-27 用计时器的计时事件改变系数a的值,并绘制相应的曲线
图16-27 用计时器的计时事件改变系数a的值,并绘制相应的曲线关于二次函数曲线的实验我们就进行到这里,读者可以发挥自己的想象力,分别对系数b、c进行类似的实验,研究系数的改变对曲线外观的影响。
第四节 绘制三角函数曲线
一、坐标轴的位置
假设我们要在0~2π之间绘制正弦曲线y=a*sinωx+θ,其中a的最大值为5,ω的取值范围为[1,3],则应采用图16- 4(c)的坐标轴来绘制曲线。需要说明的是,在App Inventor中,三角函数自变量的单位是角度,因此x的取值范围应该是[0,360]。首先确定绘制坐标轴的参数:
- (X0,Y0):(10,150)
- 比例X:0.8(在x轴正方向的290个像素的长度上,有290/0.8=362个单位)
- 比例Y:30(在原点上下150个像素的长度上,各有5个单位)
- 标注间隔X:30,即,每隔30度(24个像素)设置一个标注数字
- 标注间隔Y:1,每隔30像素设置一个标注数字
此外,还须设置a、ω及θ的值,利用三个文本输入框系数a、系数b及系数c来设置这三个值。
二、编写过程——绘制正弦函数
为了测试方便,我们在设计视图中设置好上述绘制坐标轴的参数以及三角函数曲线的参数,如图16- 28所示。
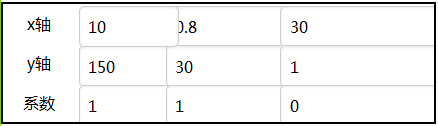 图16-28 事先设置好绘制坐标轴及曲线图的参数
图16-28 事先设置好绘制坐标轴及曲线图的参数创建一个有返回值的过程——正弦y,对于任意给定的参数x,返回值y=y=a*sinωx+θ;然后再创建“绘制正弦曲线”过程,其中循环变量的值从0至360,且增量为1;最后在绘图按钮点击程序中调用“绘制正弦曲线”过程,代码如图16- 29所示。
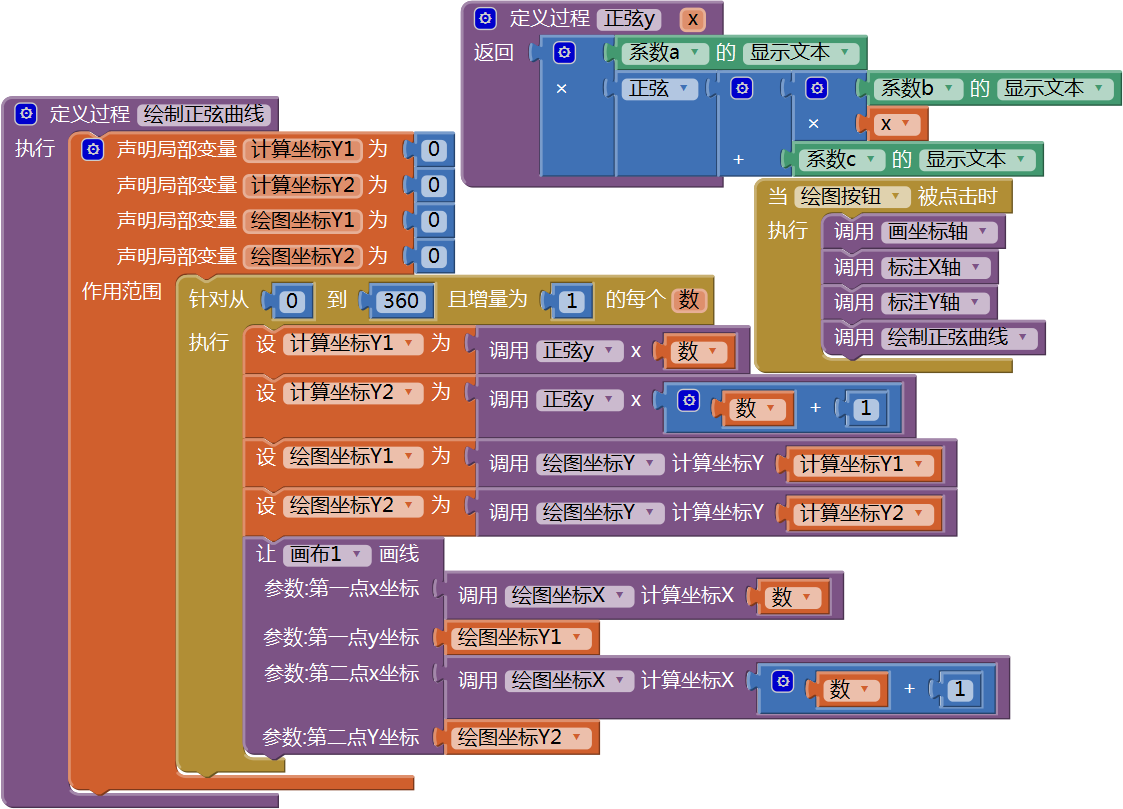 图16-29 绘制正弦曲线的相关代码
图16-29 绘制正弦曲线的相关代码在开始测试之前,除了要在文本输入框中设置相关参数外,还要记得取消勾选计时器的启用计时属性,免得计时器的计时事件触发运行绘制二次曲线程序。此外,勾选Screen1的允许滚动属性,以便屏幕底部的按钮可以显示出来,测试结果如图16- 30所示。
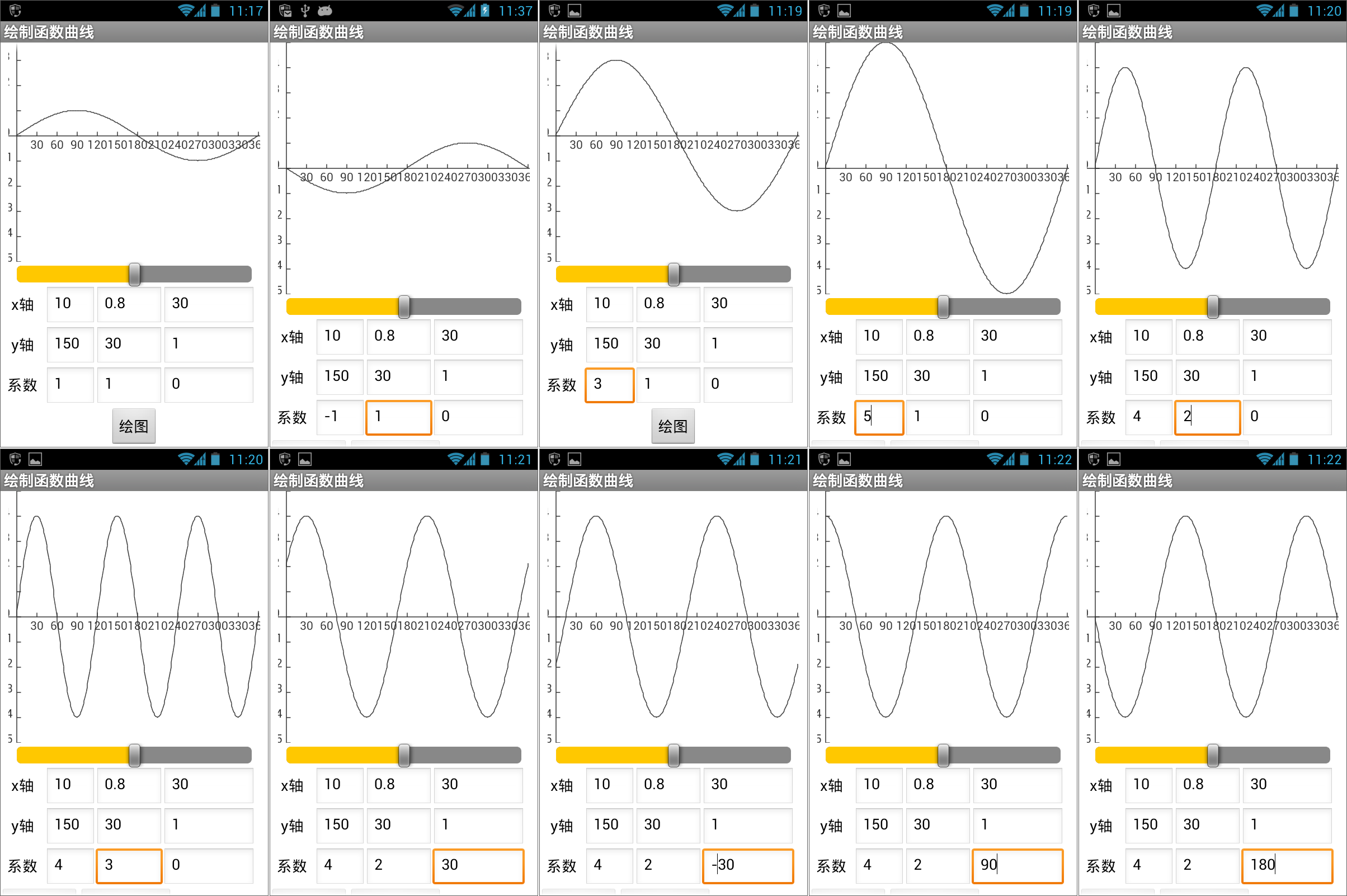 图16-30 测试——绘制不同参数下的正弦曲线
图16-30 测试——绘制不同参数下的正弦曲线测试过程中,a的取值为1、-1、3、4及5;ω的取值为1、2及3;θ的取值为0、30、-30、90及180,分别测试了三个参数对曲线位置、方向以及形状的影响。
学习过三角函数及其曲线性质的读者可以根据自己已经掌握的知识,验证一下程序绘制的图形是否正确;尚未学过相关知识的读者,可以尝试自己归纳一下曲线的形状与各个参数之间的关系。这恰好是在“实验室”中做完实验后应该完成的任务——写一份实验报告。
项目中的数字滑动条在绘制三角函数曲线时没有起到任何作用,为了节省屏幕空间,可以取消勾选它的允许显示属性。不过滑动条的存在倒是为我们的测试画面添加了一抹亮色,不妨将它保留下来。
测试过程中,点击按钮后,曲线要隔几秒钟才能显示出来,排除手机性能的因素,程序本身的计算量也比较大:360次循环,每次循环要计算两次正弦函数的值,外加一次加法运算、两次乘法运算,因此,手机的运算能力显得有些捉襟见肘。改进的思路是增大循环语句中增量的值,例如,将1改为2,这样可以将运算次数减半;或者改为5,则运算次数降为原来的五分之一,而且并不会明显地影响曲线的平滑程度(5个单位=4个像素)。
此外,由于y轴过于靠近画布左侧边缘,因此导致坐标轴的标注数字无法完整显示。在原点下方的标注数字丢掉了负号(-),而原点上方的数字则完全没有显示出来。解决的方法可以将原点向右移动10个像素,为此x轴的比例要作相应的调整,即比例x=280/360=0.777,取整后可以设为0.7。
另外,目前我们只绘制了单一颜色的一条曲线,不妨尝试用黑色画笔绘制一条基准曲线(例如y=sinx),然后再改变画笔颜色,绘制参数改变后的曲线,这样便于查看曲线特性的变化。总之,利用程序这一实验工具,你可以随心所欲地变换花样,实现各种用纸笔难于完成的试验,来满足自己对知识的好奇心。
第五节 小结
利用画布组件的画线功能,通过编写程序来绘制函数的曲线,这是一件极有趣的事情,不仅可以锻炼我们编写程序的能力,也可以加深对数学知识的理解,从而提高自己的抽象思维能力。绘制曲线过程中,涉及到许多数量关系,特归纳如下,以供参考。
- 画布尺寸——决定了可用的绘图范围;
- 函数曲线的范围(x及y的取值范围)——决定了坐标轴的原点位置、缩放比例及标注间隔;
- 影响曲线特性的参数——包括参数的个数及取值范围,需要为这些参数提供输入方法,本章中提供了三种参数输入的方式:
- 文本输入框
- 数字滑动条
- 计时器+全局变量
App Inventor的内置数学块中,提供了多种函数块,如三角函数、反三角函数、指数函数、对数函数及开方等,可以利用这些函数来绘制各种类型的曲线,也可以将这些函数进行各种组合运算,绘制复合函数的图形。需要提醒读者的是,由于手机的运算能力有限,需要考虑在不影响曲线平滑度的前提下,尽量降低运算次数。